Introduzione

Dopo aver introdotto l’isometria, possiamo affrontare un importante e delicato argomento che riguarda da vicino anche l’IA presente in un gioco. Quello di cui stiamo per parlare è : “la ricerca del percorso”.

In molti videogame il giocatore muove personalmente il suo alter-ego, senza preoccuparsi di calcolare gli spostamenti verso un dato punto. Questo purtroppo non accade per i personaggi non giocanti e nemmeno in alcune specifiche categorie di videogiochi, come per esempio gli strategici.

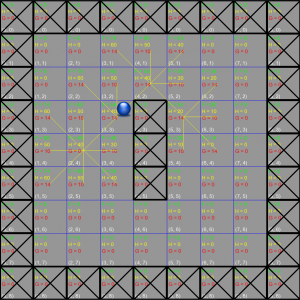
Che il gioco sia in 2D o in 3D, quello che abbiamo visto con l’isometria ci viene comunque in aiuto. Infatti, per ricercare il percorso tra due precisi punti della mappa, si cerca di suddividere quest’ultima in una griglia. Più precisamente, si costruiscono dei nodi collegati tra di loro così come sono adiacenti sul terreno. Attraversare i nodi sarà come attraversare la mappa.

Con queste poche parole però, siamo già andati molto oltre le basi spiegate in quest’articolo. Infatti ci sono dei punti che, a seconda di come sono delineati, cambiano l’esperieza di gioco :

• Tipo dei nodi (quadrati, esagoni ecc…). In questo modo cambiano il numero di figure adiacenti al singolo nodo e quindi cambia anche il modo con cui si deve scegliere il miglior percorso (anche se non di molto, solo per la parte che riguarda i nodi adiacenti).
• Come il giocatore deve percorrere il tragitto trovato
• Qualità e quantità di nodi presenti sulla mappa

Gli ultimi due punti sono molto vasti e pieni di argomenti. Per esempio, più punti sono presenti sulla mappa, più gli spostamenti saranno precisi e veritieri (ma sarà più lenta la ricerca, non dobbiamo mai dimenticare le prestazioni, visto che non si dovrebbero superare i centesimi di secondo). Inoltre bisogna considerare se il giocatore deve prevedere nei suoi spostamenti anche la presenza di altri giocatori od oggetti in movimento. Possiamo anche decidere di preferire percorsi che attraversano parti della mappa meno pericolose ed impervie. Questi sono alcune delle problematiche che possono essere sollevate.

Tutti questi piccoli aspetti, variano da gioco a gioco, anche a seconda dei gusti dei programmatori. In questo esempio vedremo solo come far muovere su una semplice mappa il nostro giocatore.

Il programma potrà essere riutilizzato per una visione isometrica, visto che la parte grafica è completamente staccata dal meccanismo della ricerca del percorso. Infatti si può “lavorare” sui nodi (le nostre piastrelle nell’esempio dell’isometria, per intenderci) come se fossero parti della mappa esistente o semplicemente facendogli formare una mappa specchio, che viede utilizzata solo per questa ricerca. In questo esempio, la mappa sarà creata e gestita come abbiamo visto per l’isometria (quindi con un array), ma graficamente scarna per far intravedere il lavoro che avviene durante la ricercare del percoso più breve.

Prima di iniziare a vedere il codice, vorrei precisare che parleremo dell’Algoritmo A* (A-Star) e che ho preparato una traduzione del sito che ho utilizzato come riferimento:

http://www.policyalmanac.org/games/aStarTutorial.htm

Ringrazio l’autore per la disponibilità.

Il tutto verrà rilasciato in fondo all’articolo. Tenete conto che la traduzione potrebbe non presentarsi bellissima in italiano, ma i concetti chiave sono presentati facilmente e vi sarà molto utile come base per le vostre implementazioni e per la lettura delle parti sottostanti. Inoltre il codice che rilascio è, per questa volta, completo di commenti, così da evitare ulteriori dubbi durante la sua lettura.

Per comodità, analizzerò solo le parti salienti, ovvero come sono costituiti i nodi e come procede l’algoritmo.

class Nodo():
    """
    Rappresenta un nodo della griglia
    """
    def __init__(self,xy,num,screen,walkable = True):
        self.xy = xy
        self.center = (xy[0]+50,xy[1]+50)
        self.rect = pygame.Rect(xy,(100,100))
        self.num = num
        self.walkable = walkable
        self.screen = screen
        self.G = 0
        self.H = 0
        self.F = 0
        self.prev = None

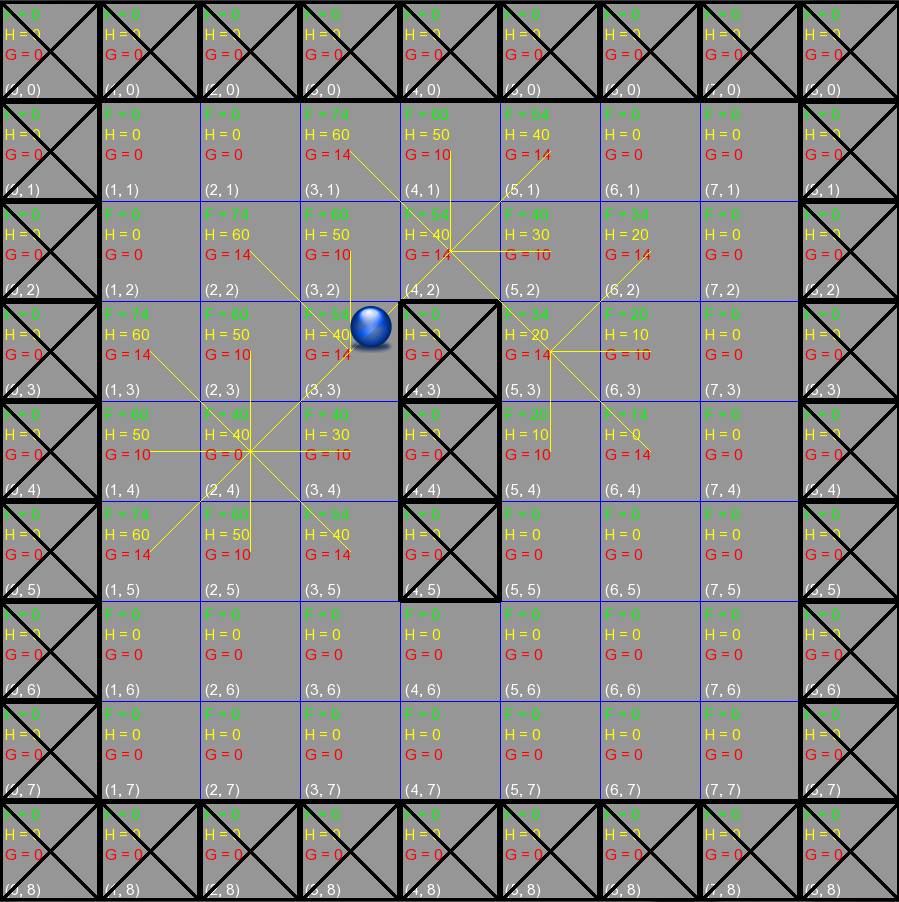
La classe nodo si trova nel file principale per eseguire il programma. Naturalmente potete posizionarla all’interno del vostro engine di gioco per affiancarla al rendering grafico. Infatti come vedete, non necessita di molte informazioni in più rispetto quelle che si dovrebbero avere per una normale piastrella della mappa. Però sono essenziali ed importantissime :

• G = Rappresenta il costo di movimento per raggiungere questo nodo, dal nodo precedente.
• H = Rappresenta il costo (o distanza) per raggiungere l’obbiettivo. Si può definire in vari metodi. Quello utilizzato in questo esempio è detto metodo di Manhattan, che calcola questa distanza sommando il numero di nodi che servono per raggiungere l’obbiettivo orizzontalmente e verticalmente e poi lo moltiplica per 10. Potete capire meglio il perché di questa operazione leggendo la traduzione del sito di riferimento che ho allegato in quest’articolo.
• F = E’ semplicemente la somma di G ed H.
• prev = Il nodo che precede quello corrente (collegati naturalmente dal percorso più breve).

Questi sono i parametri essenziali per andare avanti. Se dal codice non comprendete il procedimento e/o la logica con cui è stato affrontato il problema, vi consiglio ancora di leggere il file pdf allegato, sopratutto perché queste parti possono essere soggette a variazioni che riguardano applicazioni e/o scelte specifiche prese per un determinato gioco.

Vediamo allora come si dovrebbe procedere per cercare il nostro percorso (ed il più breve) attraverso i nodi (mappa) disponibili:

class A_Star():
    """
    Classe per la ricerca del percorso
    """
    def __init__(self,nodi,partenza,arrivo):
        """
        Inizializza l'algoritmo per la ricerca e lo esegue
        """
        if partenza is None or arrivo is None:
            return

        self.lista_aperta = []
        self.lista_chiusa = []
        self.nodi = nodi

        # Setto F,G,H del nodo di partenza
        self.nodi[partenza[1]][partenza[0]].set(arrivo)

        # Metto il nodo di partenza nella lista aperta
        heapq.heappush(self.lista_aperta,(self.nodi[partenza[1]][partenza[0]].F,self.nodi[partenza[1]][partenza[0]]))

        vicini = [] # Lista per mantenere i nodi vicini

        while len(self.lista_aperta)>0 :

            # Recupero il nodo corrente
            nodo_corrente = heapq.heappop(self.lista_aperta)

            # Controllo se il nodo corrente è l'obbiettivo
            if nodo_corrente[1].num == arrivo:
                self.lista_chiusa.append(nodo_corrente[1])
                break

            # Aggiungo il nodo corrente alla lista chiusa
            self.lista_chiusa.append(nodo_corrente[1])

            # Recupero i nodi vicini a quello corrente
            xx,yy = nodo_corrente[1].num
            del vicini[:]
            for y in range(yy-1,yy+2):
                for x in range(xx-1,xx+2):
                    if not (x == nodo_corrente[1].num[0] and y == nodo_corrente[1].num[1]):
                        if self.nodi[y][x].walkable:
                            vicini.append(self.nodi[y][x])

            # Controllo se i rimanenti si trovano nella lista aperta
            # se No, li aggiungo alla lista aperta, mettendo come padre
            # il nodo corrente.
            # se SI, confronto le G passando per il quadrato corrente
            # per vedere se c'è un percorso migliore.
            # Controllo anche se il nodo è presente nella lista chiusa
            # se SI, confronto le G passando per il quadrato corrente.
            # Quando trovo un percorso migliore, si aggiorna opportunamente
            # il nodo padre.

            for vic in vicini:
                esiste = False
                for x in self.lista_aperta:
                    if vic.num == x[1].num:
                        esiste = True
                        if (self.calcola_G(nodo_corrente[1].num,vic.num) + self.calcola_G(vic.num,x[1].num)) < x[1].G:
                            x[1].set(arrivo,vic)
                            break

                for x in self.lista_chiusa:
                    if vic.num == x.num:
                        esiste = True
                        if (self.calcola_G(nodo_corrente[1].num,vic.num) + self.calcola_G(vic.num,x.num)) < x.G:
                            x.set(arrivo,vic)
                            break

                if not esiste:
                    vic.set(arrivo,nodo_corrente[1])
                    heapq.heappush(self.lista_aperta,(vic.F,vic))

    def punti(self):
        """
        Ritorna le coordinate che il giocatore deve seguire
        """
        temp = self.lista_chiusa[-1]
        punti = []

        while temp.prev != None:
            punti.append(temp.center)
            temp = temp.prev

        return punti[::-1]

Iniziamo con il creare due liste, una denominata “aperta” ed una “chiusa”. La prima sarà gestita come un heap, così da migliorare la velocità ed il rendimento, poiché sarà molto più semplice estrarre il nodo con il più piccolo valore di F, visto che si troverà sempre in testa. Questa naturalmente è solo un’ottimizzazione, potete benissimo utilizzare le liste, magari per fare qualche esperimento.

Preparato il nodo di partenza, lo posizioniamo nella lista aperta e creiamo una lista per memorizzare i nodi adiacenti. A questo punto comincia un ciclo per ricercare il nostro percorso, che avrà come condizione di uscita o la lista aperta vuota (quindi il percorso non esiste), oppure il raggiungimento dell’obbiettivo (ed in questo caso il tragitto sarà il più breve).

Il ciclo sostanzialmente preleva il nodo con costo minore di movimento (quindi con la F più piccola) dalla lista aperta e lo mette in quella chiusa. Poi si passano al setaccio i nodi adiacenti a quello selezionato; quindi si controlla se sono già presenti in una delle due liste, per verificare l’esistenza di un percorso migliore, altrimenti si aggiungono semplicemente come prossimi candidati nella lista aperta.

Una volta completato il procedimento, la lista chiusa conterrà i nodi che dobbiamo percorrere per arrivare all’obbiettivo. In questo caso, basterà richiamare la funzione punti() per partire dall’obbiettivo ed andare a ritroso verso l’origine (ecco spiegata la presenza di prev nei nodi), memorizzando mano a mano i punti da attraversare per poi ritornarli in una comoda lista.

Conclusioni

Spero che l’articolo non sia troppo dispersivo, ma ho preferito far luce sui procedimenti e le scelte chiave, visto che è corredato da materiale molto esplicativo. L’applicazione è banale e non sono state previste molte cose. Per esempio si potrebbe utilizzare una variabile booleana per avvertire il giocatore quando il percorso non esiste e di conseguenza non far muovere il personaggio sullo schermo.

Altre varianti e/o miglioramenti sono sempre presenti nel materiale correlato. Con i prossimi articoli finiremo questo viaggio nelle due dimensioni per passare al 3D, senza staccarci da python, naturalmente…

Downloads:

• Esempio : http://tinyurl.com/6apwxe7
• A* per principianti : http://tinyurl.com/6ej2nux

L’esempio è stato compresso utilizzando 7zip. Le azioni disponibili sono le seguenti:

1. Tasto sinistro del mouse : indica nodo da raggiungere
2. Tasto centrale del mouse : resetta il contenuto dei nodi della mappa
3. Tasto destro del mouse : rende un nodo non attraversabile e viceversa